I tried implementing a text crdt in sql and in imp.
Doing this naively isn't particularly hard. The challenge here is to implement it as if writing a batch query, but in such a way that an incremental system like materialize or dida can efficiently update the result when new edits arrive. Not because this code would be particularly useful in itself, but because it helps discover the boundaries of what kinds of problems are possible to solve in this way.
The exercise is a little like GPU programming, in that avoiding sequential algorithms and shared mutable data-structures requires very carefully separating the actual essential data dependencies of the problem from those accidentally introduced by typical programming techniques.
The problem
So here is a simplified version of the problem.
We have a tree of edits, each of which represents the insert of a single character.
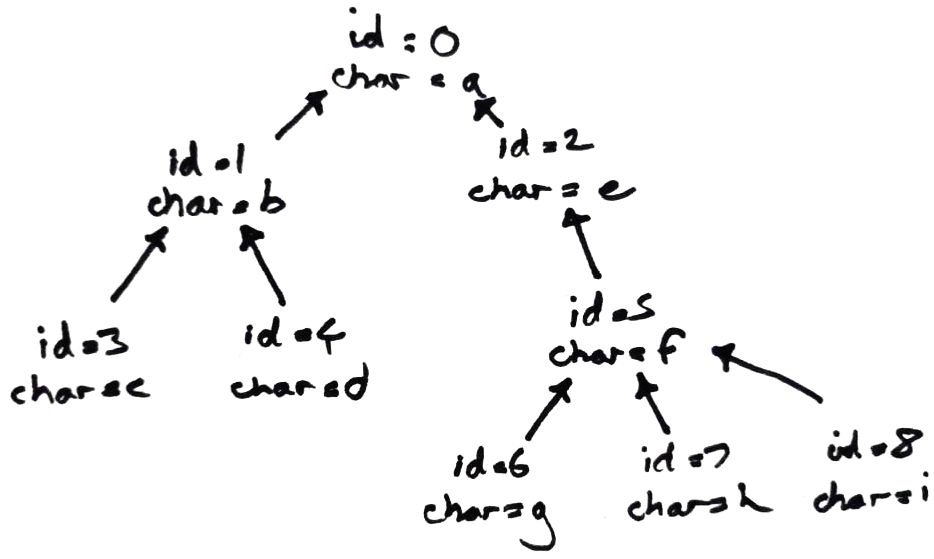
Each edit has a unique id, which for the purpose of this simple example we'll say is just an integer.
One edit is the root - the first character in the text.
Every other edit has a parent edit. The id of an edit is always greater than the id of its parent.
To construct the actual text we take this tree of edits, sort the children of each edit by id, and then do an pre-order traversal of the tree.
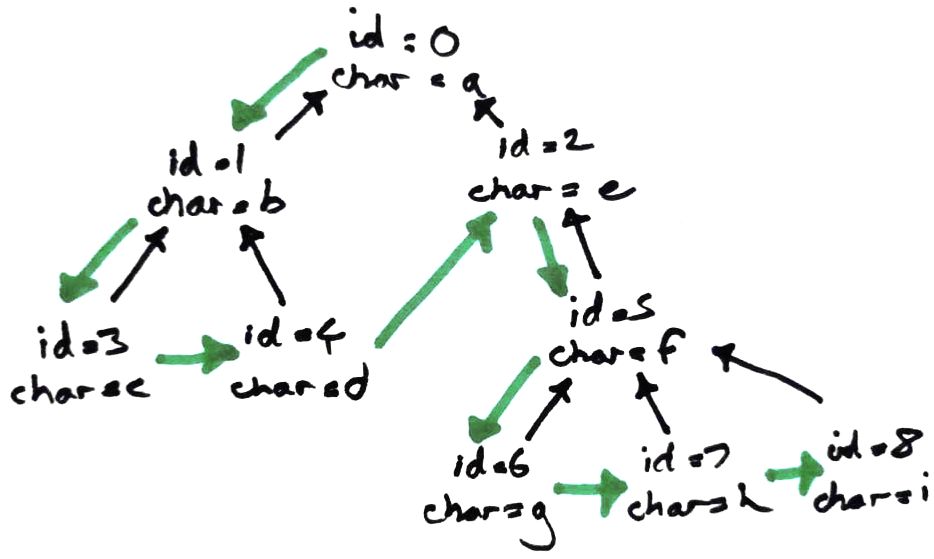
Explicit sort key
How can we implement this in sql?
create table edit(id integer, parent_id integer, character text);
insert into edit values (0, null, 'a');
insert into edit values (1, 0, 'b');
insert into edit values (2, 0, 'e');
insert into edit values (3, 1, 'c');
insert into edit values (4, 1, 'd');
insert into edit values (5, 2, 'f');
insert into edit values (6, 5, 'g');
insert into edit values (7, 5, 'h');
insert into edit values (8, 5, 'i');
Given that we're trying to sort this set of edits, the natural reaction would be to start with something like:
select * from edit order by ???;
But we're immediately stuck because there isn't an obvious sort key. The information that lets us decide whether one edit should become before or after another edit is implicit in the shape of the tree. To get an actual value to sort by, we would need to include all that information.
with recursive
path(id, path, character) as (
select edits.id, edits.id, edits.character
from edits
where edits.parent_id is null
union all
select child.id, parent.path || ',' || child.id, child.character
from edits as child, path as parent
where child.parent_id = parent.id
)
select * from path order by path.path;
0|0|a
1|0,1|b
3|0,1,3|c
4|0,1,4|d
2|0,2|e
5|0,2,5|f
6|0,2,5,6|g
7|0,2,5,7|h
8|0,2,5,8|i
This is the essence of the problem - sorting the edits by the ids in their path from the root. It's a beautiful solution, and for nicely balanced trees this would be the end of the story. But the trees for text editing crdts tend to be very deep and narrow so materializing these paths will make the storage cost look like O(N²).
(We could maybe cut this down in the typical case by only looking at parts of the path with more than one child. But the worst case would still be O(N²))
Implicit sort key
In most languages, if explicitly storing the key was too expensive we'd just sort using a custom comparison function instead.
create function compare_edits(id1 integer, id2 integer) returns comparison
as ???;
select * from edit order by comparing compare_edits(edit.id);
This isn't possible in sql today, but I could maybe add it to imp.
It would be tricky to incrementally maintain such a sort operator. The set of comparisons would probably have to be explicitly stored. It's not obvious to me how to pick pivots in a way that makes the set of required comparisons stable with respect to small changes in the input. But it might be possible.
Tree traversal
If using the builtin sort operator is not feasible, maybe we can explicitly traverse the tree ourselves.
This ends up being a little more involved:
with recursive
rightmost_child(id, parent_id) as (
select max(id), edit.parent_id
from edit
where edit.parent_id is not null
group by parent_id
),
rightmost_descendant(id, child_id) as (
select id, id
from edit
union
select parent.parent_id, child.child_id
from rightmost_child as parent, rightmost_descendant as child
where parent.id = child.id
),
rightmost_leaf(id, leaf_id) as (
select id, max(child_id) as leaf_id
from rightmost_descendant
group by id
),
prev_sibling(id, prev_id) as (
select edit.id, (
select max(sibling.id)
from edit as sibling
where edit.parent_id = sibling.parent_id
and edit.id > sibling.id
) as prev_id
from edit
where prev_id is not null
),
prev_edit(id, prev_id) as (
-- edits that have no prev siblings come after their parent
select edit.id, edit.parent_id
from edit
where not exists(
select *
from prev_sibling
where prev_sibling.id = edit.id
)
union all
-- other edits come after the rightmost leaf of their prev sibling
select edit.id, rightmost_leaf.leaf_id
from edit, prev_sibling, rightmost_leaf
where edit.id = prev_sibling.id
and prev_sibling.prev_id = rightmost_leaf.id
),
position(id, position, character) as (
-- root is at position 0
select edit.id, 0, edit.character
from edit
where edit.parent_id is null
union all
-- every other edit comes after their prev edit
select edit.id, position.position + 1, edit.character
from edit, prev_edit, position
where edit.id = prev_edit.id
and prev_edit.prev_id = position.id
)
select *
from position
order by position.position;
0|0|a
1|1|b
3|2|c
4|3|d
2|4|e
5|5|f
6|6|g
7|7|h
8|8|i
In imp it's more concise but still not particularly easy to follow:
rightmost_child: edits.?edit edit parent~ @ max;
fix rightmost_leaf: edits.?edit edit | edit rightmost_child rightmost_leaf @ max;
prev_sibling: edits.?edit edit parent parent~ .(?sibling edit > sibling) @ max;
prev: edits.?edit edit prev_sibling !! then edit prev_sibling rightmost_leaf else edit parent;
fix position: root, 0 | position ?edit ?pos edit prev~, pos + 1;
edits ?edit (edit position) , edit , (edit character)
In either case, we're likely to have to maintain at least an index on parent, parent~ and character and probably also indexes for many intermediate results too. It's somewhat concerning that it's not at all predictable from the code what those will be and how much they will cost.
In the ideal case, the output of prev is very stable and so should admit reasonably efficient incremental maintenance. But large parts of the output of position will change on every new edit, so it is inherently inefficient to maintain.
This is because prev represents the ordering implicitly, in terms of relative ordering between adjacent edits, whereas position represents the ordering explicitly by numbering each position in the sequence. In this problem, each new edit only changes the prev value of the first edit to its right, but increments the position number of every edit to its right.
Imperative solution
Here is a nice way to do this imperatively (courtesy of Seph Gentle):
- We start with an empty sequence, in which we'll store the edits in the correct order.
- We assume the edits are already sorted so that parents come before children.
- For each edit, we insert it into the sequence by first scanning the sequence to find its parent, and then scanning to the right to find the correct point to insert the child.
If the sequence is implemented as a b-tree then these scans and inserts are fairly cheap. We can also keep track of the number of characters in each branch of the b-tree so that queries like "what is the edit id for the 142nd character" can be efficiently answered by walking down the spine of the b-tree.
Explicit sequence
The imperative solution represents the ordering implicitly in terms of position in some ordered data-structure. Inserting a new edit near the beginning of the data-structure does not require explicitly updating the position of every later element - the position is implicit in the overall structure.
Can we do the same in sql?
If we switch to postgres, we can use arrays to represent the sequence.
with recursive sequence(last_id, characters, ids) as (
select edit.id, edit.character, array[edit.id]
from edit
where edit.parent_id is null
union all
select edit.id,
-- insert edit.character and edit.id at insertion_point
substring(sequence.characters, 1, insertion_point.insertion_point-1) || edit.character || substring(sequence.characters, insertion_point.insertion_point),
sequence.ids[1:insertion_point.insertion_point-1] || edit.id || sequence.ids[insertion_point.insertion_point:]
from sequence, edit
join lateral (
select coalesce(min(i), array_length(sequence.ids, 1)+1) as insertion_point
from generate_subscripts(sequence.ids, 1) as i
-- array scan for parent of edit
join lateral (
select j
from generate_subscripts(sequence.ids, 1) as j
where sequence.ids[j] = edit.parent_id)
as parent_ix on true
-- array scan for parent of ids[i]
join lateral (
select k
from generate_subscripts(sequence.ids, 1) as k, edit as o_edit
where sequence.ids[k] = o_edit.parent_id
and sequence.ids[i] = o_edit.id)
as o_parent_ix on true
-- find insertion point
where i > parent_ix.j
and o_parent_ix.k < parent_ix.j
) as insertion_point on true
where sequence.last_id + 1 = edit.id
)
select * from sequence
order by last_id desc
limit 1;
last_id | characters | ids
---------+------------+---------------------
8 | abcdefghi | {0,1,3,4,2,5,6,7,8}
(1 row)
Imp doesn't have any sequence data-structure, but we can fake one with relations to at least see what the code would look like.
// functions for working with 'arrays'
insert: ?@sequence ?position ?item
| (sequence ?old_position ?old_item
, (old_position >= position then old_position + 1 else old_position)
, old_item)
| (position, item);
find_min_pos: ?@sequence ?@cond
found: sequence ?pos ?edit cond pos edit then pos;
found @ min;
// actual crdt code
sequence:
fix (0, root) ?@sequence
next_edit: 1 + ((sequence (?pos ?edit edit)) @ max);
edits next_edit ! then sequence else
parent_pos: find_min_pos sequence@ (?pos ?edit next_edit parent edit)@;
insertion_point: find_min_pos sequence@ (?o_pos ?o_edit
o_parent_pos: find_min_pos sequence@ (?pos ?edit o_edit parent edit)@;
(o_pos > parent_pos) & (parent_pos > o_parent_pos))@;
insert
sequence@
(insertion_point!! then insertion_point else (sequence (?pos ?edit pos) @ max) + 1)
next_edit;
sequence ?pos ?edit pos, edit, (edit character)
For both the sql and imp versions it seems possible to incrementally maintain this. If we use a persistent data-structure to implement the array, then the inserts are not too expensive. If we hint to the runtime that no edits will be deleted and new edits will have increasing id numbers, then it can infer that it doesn't need to store old values of the arrays (see eg edelweiss).
On the other hand, we've introduced a completely incidental sequential dependency, lost the ability to take advantage of parallelism or vectorization, and lost the ability to handle out-of-order edits. And incremental maintenance of any downstream code might require the ability to diff successive versions of the sequence.
Conclusions, if any
There are two underlying problems here:
- The sequence is sorted by a key that is expensive to materialize or even compare. Fast imperative solutions rely on clever implicit comparisons that don't lend themselves to incremental maintenance.
- While the relative ordering of edits is stable (eg if
id=4comes beforeid=12then it will always come before it) the absolute positions are very unstable (if a new edit is inserted, the positions of everything after it must be incremented). So any explicit representation of absolute position will cause massive churn downstream.
The latter problem isn't unique to relational languages - stable ids are at the heart of any incremental maintenance problem (eg incremental algorithms in text editors often rely on pointers to tree nodes instead of character position). What makes life difficult in relational languages is that we can't use pointer identity as an id, because that requires a strongly-constrained execution order.
The shape of a btree depends on the history of operations. This allows its node ids to be more stable over time than a scheme that depends only on the current contents. So perhaps one option is to have an escape hatch that drops down to the level of inserts and deletes. At that level we can construct stable ids based on the history of operations, in a similar fashion to using tree nodes as ids into a sequence. We just have to guarantee that the details of the ids are not observable in the declarative layer so that the order of inserts/deletes does not affect the final result of the whole program.